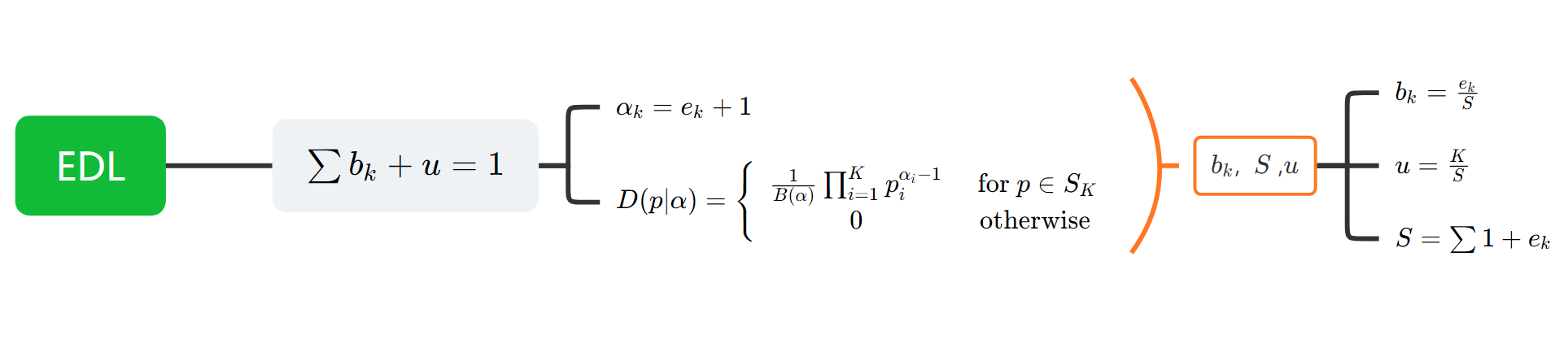论文阅读系列–损失函数改造篇
1. Evidential Deep Learning to quantify classification uncertainty
一句话摘要: 改掉Softmax替换成EDL来实现不确定性度量。
论文之我问:
1.1 这个论文的动机是什么
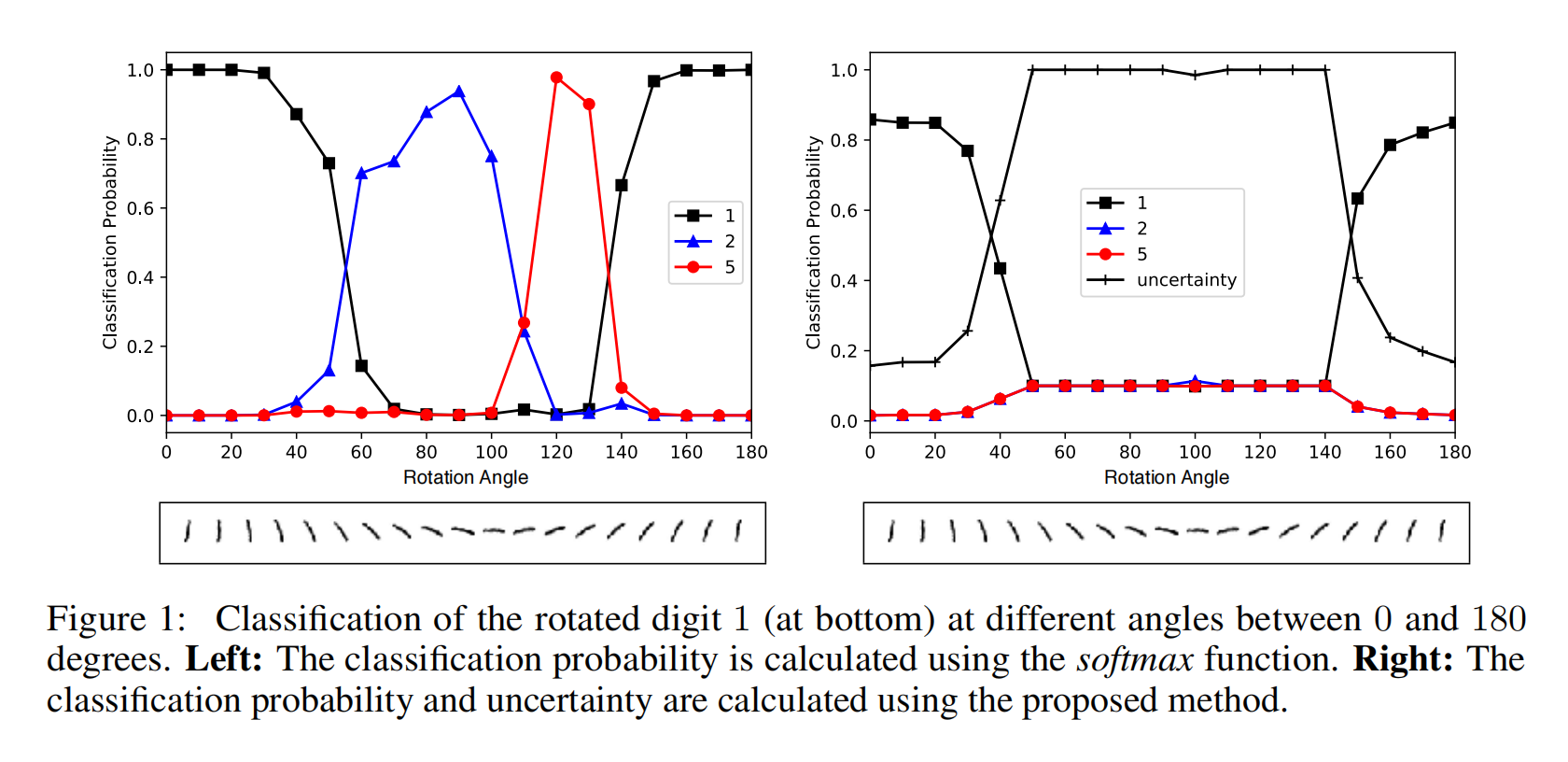
- 在本文中,作者将重点放在不确定性估计问题(uncertainty estimation (估计) problem)上,并从证据理论(Theory of Evidence)的角度来研究它[4,5]。
- 将分类网络的标准输出softmax解释为类别分布的参数集。通过用Dirichlet密度的参数替换这个参数集,我们将学习者的预测表示为可能的softmax输出的分布,而不是softmax输出的点估计。换句话说,这个密度可以直观地理解为这些点估计的工厂。所得到的模型具有一个特定的损失函数,在使用标准backprop的神经网络权值下使其最小化。
- 在一系列的实验中,证明了这种技术在两个高质量的不确定性建模至关重要的应用中比最先进的BNNs性能要好得多。具体来说,当输入来自不同于训练样本分布的输入时,我们模型的预测分布比BNNs更接近最大熵设置。
1.2 这篇论文的研究框架是什么样的
\[D ( p | \alpha ) = \left\{ \begin{array} { c c } { \frac { 1 } { B ( \alpha ) } \prod _ { i = 1 } ^ { K } p _ { i } ^ { \alpha _ { i } - 1 } } & { \text { for } p \in S _ { K } } \\ { 0 } & { \text { otherwise } } \end{array} \right.\]-
利用狄利克雷分布先验,输出的logits即为evidence, e可以被$\alpha$ 度量 \(\alpha _ { k } = e _ { k } + 1\)
-
而后我们可以确定,信念质量b,不确定性u,以及狄利克雷强度S \(S = \sum _ { i = 1 } ^ { K } \alpha _ { i }\\ b_k = \frac{e_k}{S}\\ u = \frac{K}{S}\)
-
而后我们有约束 \(u + \sum _ { k = 1 } ^ { K } b _ { k } = 1\) 当一个样本的观察结果与 K 个属性之一相关时,相应的Dirichlet参数被增加以更新Dirichlet分布与新的观察结果。例如,对图像上特定模式的检测可能有助于将其分类为特定类。在这种情况下,这个类 k 对应的Dirichlet参数应该递增。这意味着,一个样本分类的狄利克雷分布的参数可以解释每个类别的证据。